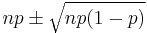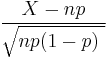Binomial distribution
Probability mass function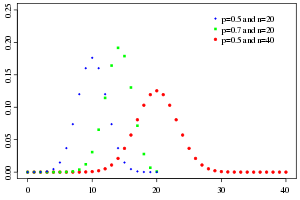 |
|
Cumulative distribution function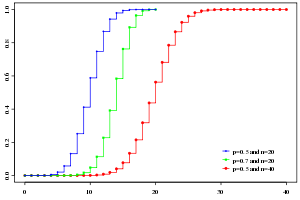 |
|
| notation: | B(n, p) |
|---|---|
| parameters: | n ∈ N0 — number of trials p ∈ [0,1] — success probability in each trial |
| support: | k ∈ { 0, …, n } |
| pmf: | 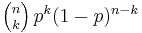 |
| cdf: | 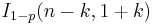 |
| mean: | np |
| median: | ⌊np⌋ or ⌈np⌉ |
| mode: | ⌊(n + 1)p⌋ or ⌊(n + 1)p⌋ − 1 |
| variance: | np(1 − p) |
| skewness: | 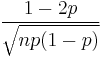 |
| ex.kurtosis: | 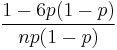 |
| entropy: | 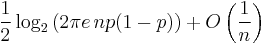 |
| mgf: | 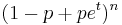 |
| cf: | 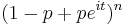 |
In probability theory and statistics, the binomial distribution is the discrete probability distribution of the number of successes in a sequence of n independent yes/no experiments, each of which yields success with probability p. Such a success/failure experiment is also called a Bernoulli experiment or Bernoulli trial. In fact, when n = 1, the binomial distribution is a Bernoulli distribution. The binomial distribution is the basis for the popular binomial test of statistical significance.
It is frequently used to model number of successes in a sample of size n from a population of size N. Since the samples are not independent (this is sampling without replacement), the resulting distribution is a hypergeometric distribution, not a binomial one. However, for N much larger than n, the binomial distribution is a good approximation, and widely used.
Contents |
Examples
An elementary example is this: roll a standard die ten times and count the number of fours. The distribution of this random number is a binomial distribution with n = 10 and p = 1/6.
As another example, flip a coin three times and count the number of heads. The distribution of this random number is a binomial distribution with n = 3 and p = 1/2.
Specification
Probability mass function
In general, if the random variable K follows the binomial distribution with parameters n and p, we write K ~ B(n, p). The probability of getting exactly k successes in n trials is given by the probability mass function:
for k = 0, 1, 2, ..., n, where
is the binomial coefficient (hence the name of the distribution) "n choose k", also denoted C(n, k), nCk, or nCk. The formula can be understood as follows: we want k successes (pk) and n − k failures (1 − p)n − k. However, the k successes can occur anywhere among the n trials, and there are C(n, k) different ways of distributing k successes in a sequence of n trials.
In creating reference tables for binomial distribution probability, usually the table is filled in up to n/2 values. This is because for k > n/2, the probability can be calculated by its complement as
So, one must look to a different k and a different p (the binomial is not symmetrical in general). However, its behavior is not arbitrary. There is always an integer m that satisfies
As a function of k, the expression ƒ(k; n, p) is monotone increasing for k < m and monotone decreasing for k > m, with the exception of one case where (n + 1)p is an integer. In this case, there are two maximum values for m = (n + 1)p and m − 1. m is known as the most probable (most likely) outcome of Bernoulli trials. Note that the probability of it occurring can be fairly small.
Cumulative distribution function
The cumulative distribution function can be expressed as:
where 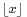 is the "floor" under x, i.e. the greatest integer less than or equal to x.
is the "floor" under x, i.e. the greatest integer less than or equal to x.
It can also be represented in terms of the regularized incomplete beta function, as follows:
For k ≤ np, upper bounds for the lower tail of the distribution function can be derived. In particular, Hoeffding's inequality yields the bound
and Chernoff's inequality can be used to derive the bound
Moreover, these bounds are reasonably tight when p = 1/2, since the following expression holds for all k ≥ 3n/8[1]
Mean and variance
If X ~ B(n, p) (that is, X is a binomially distributed random variable), then the expected value of X is
and the variance is
This fact is easily proven as follows. Suppose first that we have a single Bernoulli trial. There are two possible outcomes: 1 and 0, the first occurring with probability p and the second having probability 1 − p. The expected value in this trial will be equal to μ = 1 · p + 0 · (1−p) = p. The variance in this trial is calculated similarly: σ2 = (1−p)2·p + (0−p)2·(1−p) = p(1 − p).
The generic binomial distribution is a sum of n independent Bernoulli trials. The mean and the variance of such distributions are equal to the sums of means and variances of each individual trial:
Mode and median
Usually the mode of a binomial B(n, p) distribution is equal to ⌊(n + 1)p⌋, where ⌊ ⌋ is the floor function. However when (n + 1)p is an integer and p is neither 0 nor 1, then the distribution has two modes: (n + 1)p and (n + 1)p − 1. When p is equal to 0 or 1, the mode will be 0 and n correspondingly. These cases can be summarized as follows:
In general, there is no single formula to find the median for a binomial distribution, and it may even be non-unique. However several special results have been established:
- If np is an integer, then the mean, median, and mode coincide.[2]
- Any median m must lie within the interval ⌊np⌋ ≤ m ≤ ⌈np⌉.[3]
- A median m cannot lie too far away from the mean: |m − np| ≤ min{ ln 2, max{p, 1 − p} }.[4]
- The median is unique and equal to m = round(np) in cases when either p ≤ 1 − ln 2 or p ≥ ln 2 or |m − np| ≤ min{p, 1 − p} (except for the case when p = ½ and n is odd).[3][4]
- When p = 1/2 and n is odd, any number m in the interval ½(n − 1) ≤ m ≤ ½(n + 1) is a median of the binomial distribution. If p = 1/2 and n is even, then m = n/2 is the unique median.
Covariance between two binomials
If two binomially distributed random variables X and Y are observed together, estimating their covariance can be useful. Using the definition of covariance, in the case n = 1 we have
The first term is non-zero only when both X and Y are one, and μX and μY are equal to the two probabilities. Defining pB as the probability of both happening at the same time, this gives
and for n such trials again due to independence
If X and Y are the same variable, this reduces to the variance formula given above.
Algebraic derivations of mean and variance
We derive these quantities from first principles. Certain particular sums occur in these two derivations. We rearrange the sums and terms so that sums solely over complete binomial probability mass functions (pmf) arise, which are always unity
We apply the definition of the expected value of a discrete random variable to the binomial distribution
The first term of the series (with index k = 0) has value 0 since the first factor, k, is zero. It may thus be discarded, i.e. we can change the lower limit to: k = 1
We've pulled factors of n and k out of the factorials, and one power of p has been split off. We are preparing to redefine the indices.
We rename m = n − 1 and s = k − 1. The value of the sum is not changed by this, but it now becomes readily recognizable
The ensuing sum is a sum over a complete binomial pmf (of one order lower than the initial sum, as it happens). Thus
Variance
It can be shown that the variance is equal to (see: Computational formula for the variance):
In using this formula we see that we now also need the expected value of X 2:
We can use our experience gained above in deriving the mean. We know how to process one factor of k. This gets us as far as
(again, with m = n − 1 and s = k − 1). We split the sum into two separate sums and we recognize each one
The first sum is identical in form to the one we calculated in the Mean (above). It sums to mp. The second sum is unity.
Using this result in the expression for the variance, along with the Mean (E(X) = np), we get
Using falling factorials to find E(X2)
We have
But
So
Thus
Relationship to other distributions
Sums of binomials
If X ~ B(n, p) and Y ~ B(m, p) are independent binomial variables, then X + Y is again a binomial variable; its distribution is
Bernoulli distribution
The Bernoulli distribution is a special case of the binomial distribution, where n = 1. Symbolically, X ~ B(1, p) has the same meaning as X ~ Bern(p). Conversely, any binomial distribution, B(n, p), is the sum of n independent Bernoulli trials, Bern(p), each with the same probability p.
Normal approximation
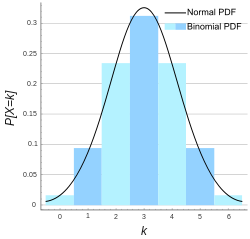
If n is large enough, then the skew of the distribution is not too great. In this case, if a suitable continuity correction is used, then an excellent approximation to B(n, p) is given by the normal distribution
The approximation generally improves as n increases (at least 20) and is better when p is not near to 0 or 1.[6] Various rules of thumb may be used to decide whether n is large enough, and p is far enough from the extremes of zero or unity:
- One rule is that both x=np and n(1 − p) must be greater than 5. However, the specific number varies from source to source, and depends on how good an approximation one wants; some sources give 10 which gives virtually the same results as the following rule for large n until n is very large (ex: x=11, n=7752).
- That rule[6] is that for
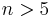 the normal approximation is adequate if
the normal approximation is adequate if
- Another commonly used rule holds that the normal approximation is appropriate only if everything within 3 standard deviations of its mean is within the range of possible values, that is if
- Also as the approximation generally improves, it can be shown that the inflection points occur at
The following is an example of applying a continuity correction: Suppose one wishes to calculate Pr(X ≤ 8) for a binomial random variable X. If Y has a distribution given by the normal approximation, then Pr(X ≤ 8) is approximated by Pr(Y ≤ 8.5). The addition of 0.5 is the continuity correction; the uncorrected normal approximation gives considerably less accurate results.
This approximation, known as de Moivre–Laplace theorem, is a huge time-saver (exact calculations with large n are very onerous); historically, it was the first use of the normal distribution, introduced in Abraham de Moivre's book The Doctrine of Chances in 1738. Nowadays, it can be seen as a consequence of the central limit theorem since B(n, p) is a sum of n independent, identically distributed Bernoulli variables with parameter p. This fact is the basis of a hypothesis test, a "proportion z-test," for the value of p using x/n, the sample proportion and estimator of p, in a common test statistic.[7]
For example, suppose you randomly sample n people out of a large population and ask them whether they agree with a certain statement. The proportion of people who agree will of course depend on the sample. If you sampled groups of n people repeatedly and truly randomly, the proportions would follow an approximate normal distribution with mean equal to the true proportion p of agreement in the population and with standard deviation σ = (p(1 − p)/n)1/2. Large sample sizes n are good because the standard deviation, as a proportion of the expected value, gets smaller, which allows a more precise estimate of the unknown parameter p.
Poisson approximation
The binomial distribution converges towards the Poisson distribution as the number of trials goes to infinity while the product np remains fixed. Therefore the Poisson distribution with parameter λ = np can be used as an approximation to B(n, p) of the binomial distribution if n is sufficiently large and p is sufficiently small. According to two rules of thumb, this approximation is good if n ≥ 20 and p ≤ 0.05, or if n ≥ 100 and np ≤ 10.[8]
Limits
- As n approaches ∞ and p approaches 0 while np remains fixed at λ > 0 or at least np approaches λ > 0, then the Binomial(n, p) distribution approaches the Poisson distribution with expected value λ.
- As n approaches ∞ while p remains fixed, the distribution of
- approaches the normal distribution with expected value 0 and variance 1 (this is just a specific case of the Central Limit Theorem).
Generating binomial random variates
- Luc Devroye, Non-Uniform Random Variate Generation, New York: Springer-Verlag, 1986. See especially Chapter X, Discrete Univariate Distributions.
- doi:10.1145/42372.42381
This citation will be automatically completed in the next few minutes. You can jump the queue or expand by hand
See also
- Bean machine / Galton box
- Beta distribution
- Binomial proportion confidence interval
- Hypergeometric distribution
- Logistic regression
- Multinomial distribution
- Negative binomial distribution
- Beta-binomial distribution
- Normal distribution
- Poisson distribution
- Sample_size#Estimating_proportions
- SOCR
References
- ↑ Matousek, J, Vondrak, J: The Probabilistic Method (lecture notes) [1].
- ↑ Neumann, P. (1966). "Über den Median der Binomial- and Poissonverteilung" (in German). Wissenschaftliche Zeitschrift der Technischen Universität Dresden 19: 29–33.
- ↑ 3.0 3.1 Kaas, R.; Buhrman, J.M. (1980). "Mean, Median and Mode in Binomial Distributions". Statistica Neerlandica 34 (1): 13–18. doi:10.1111/j.1467-9574.1980.tb00681.x.
- ↑ 4.0 4.1 doi:10.1016/0167-7152(94)00090-U
This citation will be automatically completed in the next few minutes. You can jump the queue or expand by hand - ↑ Morse, Philip (1969). Thermal Physics. New York: W. A. Benjamin. ISBN 0805372024.
- ↑ 6.0 6.1 Box, Hunter and Hunter (1978). Statistics for experimenters. Wiley. p. 130.
- ↑ NIST/SEMATECH, "7.2.4. Does the proportion of defectives meet requirements?" e-Handbook of Statistical Methods.
- ↑ NIST/SEMATECH, "6.3.3.1. Counts Control Charts", e-Handbook of Statistical Methods.
External links
- Web Based Binomial Probability Distribution Calculator (does not require java)
- Binomial Probabilities Simple Explanation
- SOCR Binomial Distribution Applet
- CAUSEweb.org Many resources for teaching Statistics including Binomial Distribution
- "Binomial Distribution" by Chris Boucher, Wolfram Demonstrations Project, 2007.
- Binomial Distribution Properties and Java simulation from cut-the-knot
- Statistics Tutorial: Binomial Distribution
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||
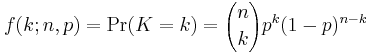
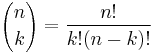
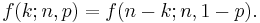
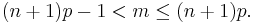
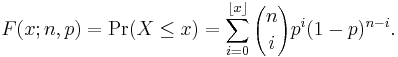
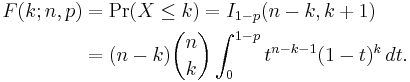
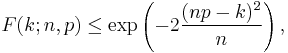
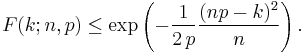
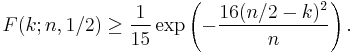
![\operatorname{E}[X] = np](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/470417702b45747e83aa8e85f8320cbc.png)
![\operatorname{Var}[X] = np(1 - p).](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/6911427653233b5f214b3116dbe505c2.png)
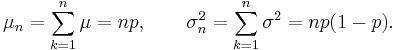
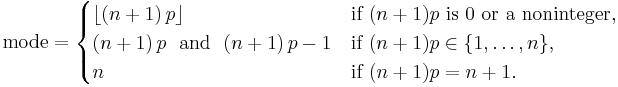
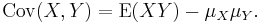
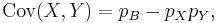
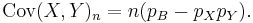
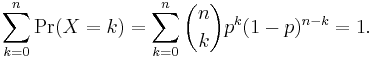
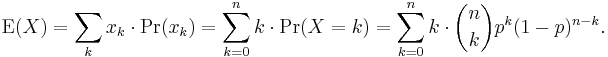
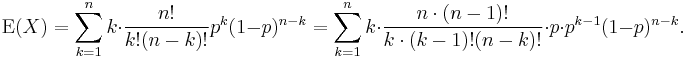
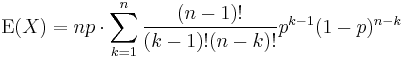
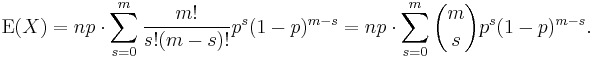
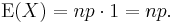
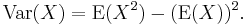
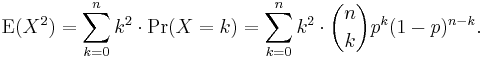
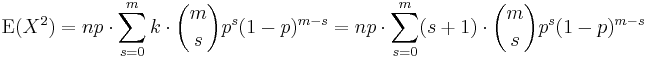
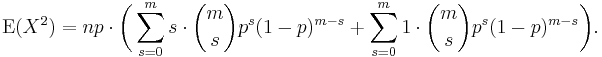
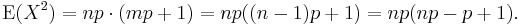
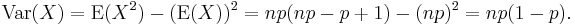
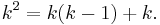
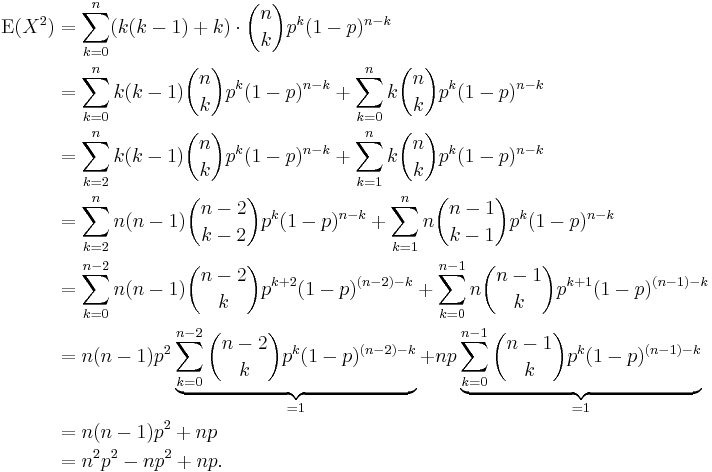
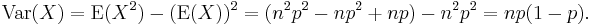
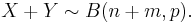
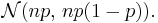
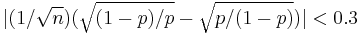
![\mu \pm 3 \sigma = np \pm 3 \sqrt{np(1-p)} \in [0,n]. \,](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/dbd317d2ca76aa7198361caf51d185c0.png)